Expectation–Maximization (EM) Clustering using Gaussian Mixture Models (GMM)

With Gaussian Mixture Models (GMMs) we assume that the data points are Gaussian distributed. In order to find the parameters of the Gaussian for each cluster (e.g the mean and standard deviation) we will use an optimization algorithm called Expectation–Maximization (EM).

1. Select the number of clusters and randomly initializing the Gaussian distribution parameters for each cluster.
2. Given these Gaussian distributions for each cluster, compute the probability that each data point belongs to a particular cluster.  
3. Based on these probabilities, we compute a new set of parameters for the Gaussian distributions such that we maximize the probabilities of data points within the clusters. We compute these new parameters using a weighted sum of the data point positions, where the weights are the probabilities of the data point belonging in that particular cluster.

Advantage

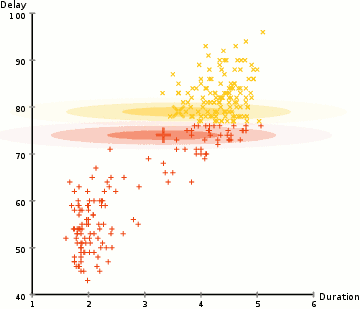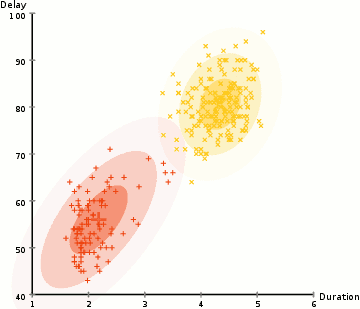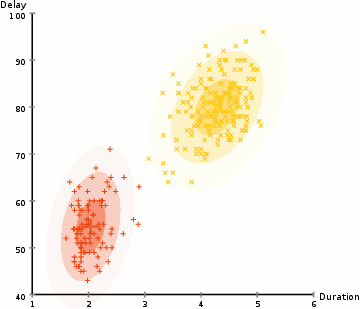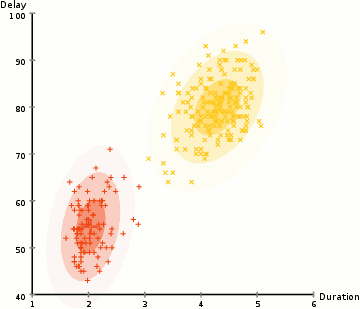
1. More flexible in terms of cluster covariance than K-Means; due to the standard deviation parameter, the clusters can take on any ellipse shape, rather than being restricted to circles.
2. Since GMMs use probabilities, they can have multiple clusters per data point. So if a data point is in the middle of two overlapping clusters, we can simply define its class by saying it belongs X-percent to class 1 and Y-percent to class 2. GMMs support mixed membership.

source: The 5 Clustering Algorithms Data Scientists Need to Know