Unsupervised Learning (Machine Learning)

Unsupervised Learning

Unsupervised learning is called “unsupervised” because you start with unlabeled data. Unsupervised learning is often used to preprocess the data. Usually, that means compressing it in some meaning-preserving way like with principal component analysis (PCA) or singular value decomposition (SVD) before feeding it to a deep neural net or another supervised learning algorithm.

Clustering

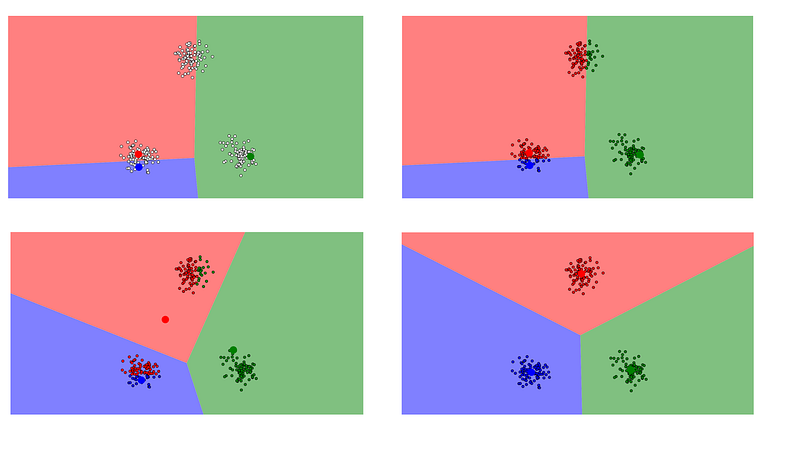
The goal of clustering is to create groups of data points such that points in different clusters are dissimilar while points within a cluster are similar.

k-means clustering

With k-means clustering, we want to cluster our data points into k groups. A larger k creates smaller groups with more granularity, a lower k means larger groups and less granularity.

The output of the algorithm would be a set of “labels” assigning each data point to one of the k groups. In k-means clustering, the way these groups are defined is by creating a centroid for each group. The centroids are like the heart of the cluster, they “capture” the points closest to them and add them to the cluster.

hierarchical clustering

Hierarchical clustering is similar to regular clustering, except that you’re aiming to build a hierarchy of clusters. This can be useful when you want flexibility in how many clusters you ultimately want. In addition to cluster assignments you also build a nice tree that tells you about the hierarchies between the clusters.

Dimensionality reduction

Dimensionality reduction looks a lot like compression. This is about trying to reduce the complexity of the data while keeping as much of the relevant structure as possible. 

principal component analysis (PCA)

PCA remaps the space in which our data exists to make it more compressible. The transformed dimension is smaller than the original dimension. This is the promise of dimensionality reduction: reduce complexity (dimensionality in this case) while maintaining structure (variance).

singular value decomposition (SVD)

SVD is a computation that allows us to decompose a big matrix into a product of 3 smaller matrices (U=m x r, diagonal matrix Σ=r x r, and V=r x n where r is a small number). The values in the r*r diagonal matrix Σ are called singular values. What’s cool about them is that these singular values can be used to compress the original matrix. If you drop the smallest 20% of singular values and the associated columns in matrices U and V, you save quite a bit of space and still get a decent representation of the underlying matrix.

source: Machine Learning for Humans, Part 3: Unsupervised Learning